Quel est le nombre de rotations minimum nécessaire permettant de résoudre un rubik's cube?

Est appelé algorithme de Dieu l'algorithme ( = enchaînement de rotations exécutées sur le cube dans un but précis) qui permettrait de résoudre le rubik's cube à partir de n'importe lequel de ses états (et Dieu seul sait qu'il sont nombreux), en un nombre minimum de mouvements. Cet algorithme n'a pas été trouvé à l'heure actuelle. Il est estimé par plusieurs méthodes que le nombre minimum de mouvements serait aux alentours de vingt.

Nous avons ainsi cherché des méthodes qui pouvaient faire apparaître le nombre de rotations minimum et qui étaient accessibles à notre niveau de connaissances.

  1. Suite.

    2. Voici un extrait d'une page de Wikipédia ( disponible ici ) sur lequel nous avons travaillé pendant quelques temps :
    "À partir de ces mouvements, on peut construire un arbre où chaque nœud représente une position du cube (la permutation appliquée au cube résolu). En partant de l’identité, on peut construire une suite (Sn) qui à chaque étape est égal au nombre de position possible du cube réalisable avec n mouvements de base. On a S0 = 1,S1 = 18,S2 = 18 * 18 + 27 et ensuite pour tout n, on a Sn = 12Sn - 1 - 18Sn - 2. En effet, pour plus de précision dans le calcul, il ne faut bien entendu pas compter toutes les permutations qui permettraient de revenir à une position déjà atteinte. Pour cela, il faut donc fixer des conditions (on compte ici les mouvements de la tranche du milieu) : on ne compte pas les positions obtenues par deux mouvements consécutifs sur une même face ni trois mouvements due le même axe."

    Nous n'avons cependant pas compris l'origine des nombres composants cette suite définie par récurrence. Nous ignorons également si nous pouvons nous fier à cet article tiré de Wikipédia.

    Nous allons tout de même apporter quelques précisions sur la suite : Sn = 12Sn - 1 - 18Sn - 2 avec S0=1; S1=18 et S2=351.
    Nous pouvons facilement montrer que cette suite n'est ni géométrique, ni arithmétique:
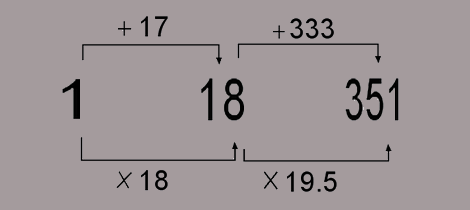
    suite

  2. Fonction logarithme.

    3. Le nombre de transformations élémentaires du rubik's cube est 18. Voilà pourquoi : Rubik's cube'
    F (front), U (up) et R (right) sont trois transformations élémentaires ou rotations que nous pouvons effectuer. A ces trois rotations correspondent leurs inverses (rotations dans l'autres sens = F', U' ou R'). Puis, par exemple, U peut s'appliquer à la couronne centrale mais aussi à la couronne du bas. On parlera alors respectivement de E (equatorial) et de D (down). Ce principe s'applique à F et R (mais les appellations changent). On dénombre alors 18 transformations élémentaires (2 × 3²).

    Il serait tentant de dire que X rotations effectuées à la suite permettraient d'obtenir X états du cube différents. Cependant il n'en est rien. En effet, il se peut qu'à une rotation, nous obtennions un état déjà obtenu auparavant par une des rotations précédentes. Si nous effectuons la rotation d'une face dans le sens direct, puis la rotation de la même face dans le sens indirect, nous retomberons alors sur un état déjà obtenu. La formule 18X pourrait compter deux états au lieu d'un. Il faut donc trouver une formule qui prenne en compte cette situation.
    Cette formule n'est autre que : A(x) = 18 × 17X-1.
    De plus, en résolvant l'équation A(x) = 4.319, nous trouverons le nombre de rotations nécessaires à effectuer pour atteindre n'importe quel état du rubik's cube. S'il est possible d'atteindre tous les états avec le nombre X de mouvements, X doit également être le nombre permettant de résoudre le rubik's cube quelque soit sa configuration.

    MAIS, cette formule possède un défaut plutôt génant. Eh oui, qu'arriverait-il si par mégarde, nous faisions une rotation U suivie de D, U'et D' (qui sont les inverses de U et D) ? Le résultat est simple, nous reviendrions à l'état du cube qui précède la rotation U, et pourtant, nous n'avons pas exécuté une rotation et son inverse à la suite. Cela veut dire que cette formule "surestime" le nombre d'états distincts atteints pour X rotations. Effectivement, des états seront comptabilisés plusieurs fois. Nous exploiterons tout de même cette formule pour résoudre l'équation.

  3. Utilisation d'Excel.

tableau_suite-fonction

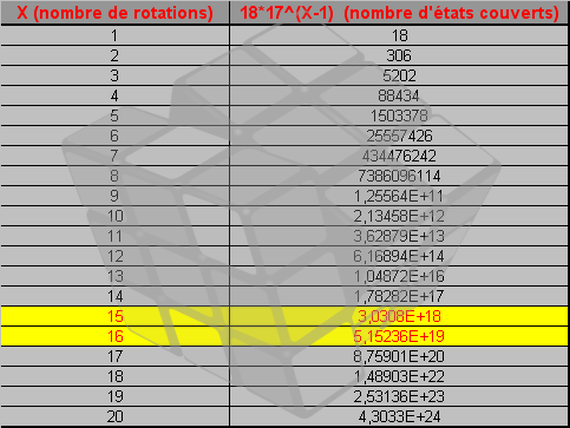
Nous avons, grâce à Excel, trouvé une approximation de X pour l'équation logarithmique ( A(x) = 4.319 ). X serait situé entre 15 et 16. C'est-à-dire que 16 rotations sont suffisantes pour résoudre le rubik's cube depuis n'importe lequel de ses états. Nous pouvons aussi affirmer qu'un cube est bien mélangé dès que 16 rotations ont été réalisées.
NB : Cette interprétation est faussée à cause de la formule inexacte. Cela nous permet tout de même d'affirmer que le nombre X est supérieur à 16. En effet, nous avons vu que la formule prenait en compte des états du Rubik's cube plusieurs fois; nous imaginons alors que la réelle formule devrait être plus "petite". Donc le nombre X devrait être plus grand pour arriver à 4.319.

Analyse des outils mathématiques et mystiques liés à la résolution du Rubik's cube.